A random number with a Gaussian distribution expression
A random number with a gaussian distribution is a weighted random expression similar to the Weighted Choose. It takes two values, a mean and a standard deviation, and returns a value close to the mean more often than values far away.
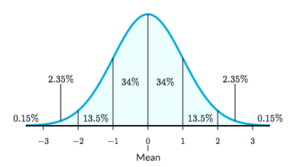
A gaussian distribution (also known as normal distribution) is a type of distribution that represents a bell curve. The area below the bell curve defines the probability of its values.
Mean and Standard Deviation
Mean represents the central value of the normal distribution. A gaussian distribution with a mean of 1 will have 1 as the center of the curve.
Standard Deviation represents the interval of values from the mean moving outwards. A gaussian distribution with a standard distribution of 2 will multiply the intervals to 2 (values 0 to -2 and 0 to 2 will have a 34% chance, values -2 to -4 and 2 to 4 will have a 14% chance, etc.). A higher standard deviation (greater than 1) will flatten the bell curve, and the probabilities of the values around e mean will became more similar. A lower standard deviation (lower than 1) will squeeze the bell curve, and the probabilities of the values close to the mean will increase, and the values far from the mean will decrease. A standard deviation of 0 will return only the value of the mean. Standard Deviations cannot be negative.