A random number with a Gaussian distribution expression
A random number with a Gaussian distribution is an Expression for adding randomness near a center value.
This expression takes two values, a mean and a standard deviation, and returns a value close to the mean more often than values far away.
You might also know gaussian distribution by other names, such as normal distribution or bell curve.
Why it's useful in games
The gaussian distribution is useful when you want to represent randomness as a "center" value (the average) with some jitter on either side. There are lots of cases where something is best expressed as "About N, plus or minus M". Here are some examples:
- You want to launch an arrow approximately upwards, but the archer is a little bit inaccurate. One way of thinking of this is that the arrow's angle is about 90 degrees, but might be a few degrees crooked to the left or right. You could represent this as a gaussian expression with a mean of 90 and a standard deviation of 3.
- You have a camp fire which creates smoke, and you want the smoke to mostly appear centered on the fire, but a little bit to either side. You might use gaussian distributions for the relative X and Y position of the smoke: Repeat every 0.5 seconds: Create actor Smoke at relative position: (Gauss(0, 1), Gauss(0, 1)). The "center" is (0, 0), but the smoke will, over time, appear in a range around the center.
Many naturally occurring physical processes and phenomena tend to follow a gaussian distribution, so some people prefer this expression just because it looks more realistic.
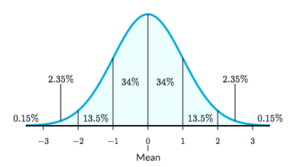
Mean and Standard Deviation
Mean represents the central value of the normal distribution. A gaussian distribution with a mean of 1 will have 1 as the center of the curve.
Standard Deviation represents the interval of values from the mean moving outwards. A gaussian distribution with a standard distribution of 2 will multiply the intervals to 2 (values 0 to -2 and 0 to 2 will have a 34% chance, values -2 to -4 and 2 to 4 will have a 14% chance, etc.). A higher standard deviation (greater than 1) will flatten the bell curve, and the probabilities of the values around e mean will became more similar. A lower standard deviation (lower than 1) will squeeze the bell curve, and the probabilities of the values close to the mean will increase, and the values far from the mean will decrease. A standard deviation of 0 will return only the value of the mean. Standard Deviations cannot be negative.